贝叶斯定理

1 简介

贝叶斯定理是18世纪英国数学家[托马斯·贝叶斯(Thomas Bayes)提出得重要概率论理论.

“正向概率”，如“假设袋子里面有 N 个白球，M 个黑球，你伸手进去摸一把，摸出黑球的概率是多大”。

反问题：“如果我们事先并不知道袋子里面黑白球的比例，而是闭着眼睛摸出一个（或好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。

这个问题，就是所谓的逆向概率问题。

2 定义

贝叶斯定理：

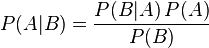
    P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。

    P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。

    P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。

    P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。

    P(B|A)/P(B)也有时被称作标淮相似度（standardised likelihood）

即：后验概率 = (相似度 先验概率)/标淮化常量= 标淮相似度 先验概率

条件概率：事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。

联合概率：两个事件共同发生（数学概念上的交集）的概率。A 与 B 的联合概率表示为联合概率。

3 推导

B 发生的条件下事件 A 发生的概率为：

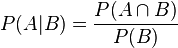
A 发生的条件下事件 B 发生的概率为：

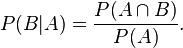
联合来看：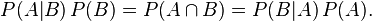

带入：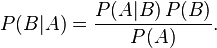

溯源

事件 A 在事件 B 发生的条件下的概率，与事件 B 在事件 A 发生的条件下的概率是不一样的；贝叶斯定理就是这种关系的陈述，可以依靠与该事件本质属性相关的事件发生的概率去推测该事件发生的概率

两孩概率问题

一个家庭有两个孩子，已知一个是女孩，求另一个也是女孩的概率

是在已经知道家庭中有两个孩子情况下来了解概率的，因此他们的概率为1/3

三门问题（Monty Hall problem）

参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。

问题是：换另一扇门会否增加参赛者赢得汽车的概率？

不换门的赢得汽车的概率是1/3，换门赢得汽车的概率是2/3。
确实是有点反直觉的问题~